Apprendre les tables d’addition peut être un véritable défi, que ce soit au CP ou au CE1. Dans cet article, je vous propose une méthode progressive pour aider vos élèves à les mémoriser en douceur, sans stress. Fini les répétitions monotones qui ne donnent aucun sens et n’aident pas à la mémorisation. Les fiches mémos jointes permettront également de poursuivre le travail à la maison.
Ne pas connaître ses tables d’addition peut rapidement devenir préjudiciable, notamment lorsqu’il s’agit de réaliser des calculs plus complexes, comme 38+46 ou même 56+7. J’accompagne actuellement des élèves de CM1 qui se retrouvent perdus dès qu’il s’agit de calculer. Ils perdent un temps précieux à compter sur leurs doigts et ne savent souvent plus où ils en sont. J’ai donc réalisé qu’il était inutile de s’attarder sur la valeur positionnelle des chiffres tant que les tables n’étaient pas acquises. J’ai donc réfléchi à une méthode de mémorisation basée sur l’observation des termes d’une somme.
Pour mes séances, j’utilise des cartes additives. Au départ, je montre la pile de cartes en expliquant l’objectif final : être capable de donner le résultat de chaque somme le plus rapidement possible.
Avant cela, je sélectionne toutes les sommes du type +0, +1 et leur inverse. Je réalise ensuite une petite séance de “calcul flash”. Évidemment, les élèves trouvent cela facile et s’exclament : “Pff, trop facile !” Je leur demande alors d’expliquer pourquoi c’est si simple :
- “+0” signifie qu’on n’ajoute rien, donc on garde le nombre initial de l’addition.
- “+1” signifie qu’on obtient le nombre qui suit.
À ce moment-là, je sors un tableau de Pythagore contenant toutes les additions des nombres de zéro à dix. Je propose aux élèves de colorier les cases correspondant aux sommes +0 et +1. Cela signifie que ces sommes ne posent aucun problème de calcul.
La même démarche est ensuite répétée avec les sommes +2 et +3. Je propose à chaque élève de trouver sa propre méthode de calcul. Par exemple, pour 9+2, certains élèves ont tendance à compter sur leurs doigts, tandis que d’autres réalisent mentalement l’opération en avançant de 2.
Une fois que la démarche est intégrée, je propose divers exercices de rapidité, comme compter de deux en deux à partir d’un nombre donné ou demander aux élèves de donner instantanément le résultat de N+2 lorsqu’on leur présente une carte-nombre. L’entraînement se poursuit ensuite avec les sommes +3.
Pour la suite, les élèves sortent leur tableau de Pythagore et peuvent colorier les cases correspondant aux sommes +2 et +3. À ce stade, plus de la moitié du tableau est déjà coloriée. Normalement, les élèves connaissent déjà les doubles jusqu’à 5+5.
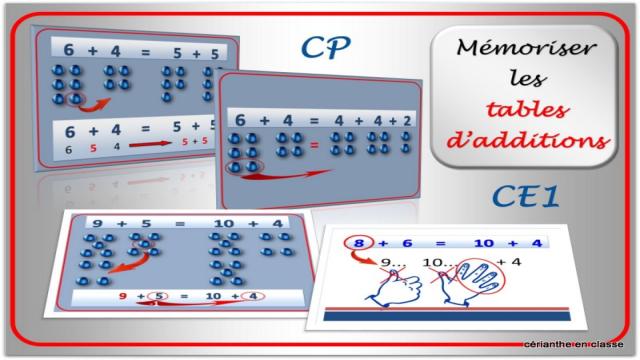
Dans un premier temps, j’étale sur la table les cartes suivantes : 2+3, 3+4, 4+5, 5+6 et leur inverse. Je demande aux élèves de trouver la particularité de ces sommes. Il s’agit de nombres qui se suivent. L’objectif est de les amener à remarquer que ces sommes sont proches des doubles. Par exemple, 3+4 peut être vu comme (3+3)+1, et 5+4 peut être vu comme (5+5)-1.
Dans un deuxième temps, j’étale les cartes 1+3, 2+4, 3+5, 4+6 et leur inverse. J’invite les élèves à trouver ce que ces sommes ont en commun. Il y a un écart de 2 entre les nombres. Ainsi, si on enlève 1 au plus grand des deux nombres et qu’on l’ajoute au plus petit, on obtient un double.
La séance se termine par un exercice de calcul rapide en deux temps. Les cartes étudiées sont mélangées et les élèves doivent reformuler la règle issue de leurs observations pour ensuite effectuer le calcul mentalement.
Pour la séance suivante, les élèves sont invités à apprendre les doubles jusqu’à 9+9. Le déroulement est identique à la séance précédente.
Arrivés à un stade avancé, il reste peu de cases non coloriées dans le tableau. Les cartes-sommes correspondantes sont étalées sur la table et les élèves doivent trouver une technique de calcul. Par exemple, pour 8+6, on peut utiliser la méthode des doigts en préparant six doigts et en comptant à partir de huit jusqu’à dix. Ensuite, il suffit de calculer 10+ le nombre de doigts restants.
Certains élèves ont tendance à s’accrocher à une méthode au point d’en oublier les autres, même quand elles sont plus simples. Pour pallier cela, j’ai créé des fiches-mémos qui sont utilisées pendant la séance. Une carte est tirée au hasard et le groupe doit trouver toutes les façons possibles de faire le calcul en se référant aux fiches.
Au fur et à mesure des séances, le tableau d’addition se remplit de plus en plus. Les élèves continuent d’apprendre les compléments à dix et de trouver des techniques de calcul pour les dernières cases non coloriées.
Cette méthode progressive permet aux élèves de mémoriser les tables d’addition de manière efficace et sans stress. La semaine prochaine, ils auront droit à un grand jeu de synthèse reprenant les principales techniques étudiées. À bientôt !