L’assurance automobile est essentielle pour assurer la sécurité et la tranquillité d’esprit sur la route. Mais comment les compagnies d’assurance déterminent-elles le coût moyen des sinistres ? Dans cet article, nous allons explorer la modélisation du coût moyen des sinistres en assurance automobile à l’aide de modèles linéaires généralisés (GLM).
Introduction aux modèles linéaires généralisés
Les modèles linéaires généralisés (GLM) sont une extension du modèle de régression linéaire. Ils permettent de modéliser une variable dépendante en fonction d’un ensemble de variables explicatives lorsque la variable dépendante suit une loi de probabilité appartenant à la famille exponentielle. Ils sont utilisés lorsque la relation entre la variable dépendante et les variables explicatives n’est pas linéaire ou lorsque la variable dépendante n’est pas continue.
Un modèle GLM est composé de trois éléments : la composante aléatoire, le prédicateur linéaire et la fonction lien. La composante aléatoire identifie la distribution de probabilités de la variable à expliquer. Le prédicateur linéaire est la composante déterministe du modèle et est calculé à partir des variables explicatives. La fonction lien exprime la relation fonctionnelle entre la composante aléatoire et le prédicateur linéaire.
Modélisation du coût risque en assurance automobile
Dans notre étude, nous cherchons à modéliser la variable endogène “coût risque” en fonction de deux variables explicatives : l’âge du conducteur et la région. Nous avons utilisé deux modèles GLM, l’un avec une loi gamma et l’autre avec une loi normale.
Modèle à loi gamma
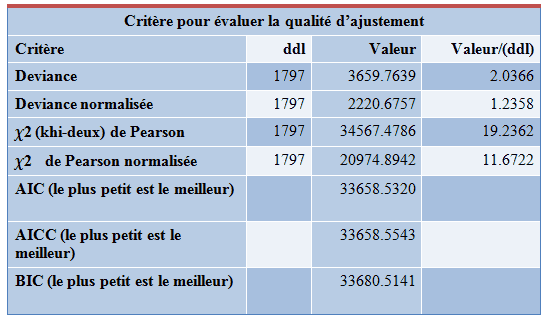
Dans le modèle à loi gamma, nous supposons que la variable “coût risque” suit une loi gamma. La fonction lien est donnée par le logarithme. Les résultats montrent que l’hypothèse de la loi gamma est à rejeter, car la valeur de la statistique khi-deux de Pearson normalisée est largement supérieure à 1. Cela remet en question l’adéquation du modèle.
Modèle à loi normale
Dans le modèle à loi normale, nous supposons que la variable “coût risque” suit une loi normale. La fonction lien est l’identité. Les résultats indiquent que l’hypothèse de la loi normale est acceptable, car la déviance normalisée et la valeur de la statistique khi-deux de Pearson normalisée sont proches de 1. Cela suggère que le modèle à loi normale est une bonne approximation du coût moyen des sinistres en assurance automobile.
Conclusion
La modélisation du coût moyen des sinistres en assurance automobile à l’aide de modèles linéaires généralisés permet de mieux comprendre les facteurs qui influencent ce coût. Dans notre étude, nous avons examiné les modèles à loi gamma et à loi normale. Les résultats ont montré que le modèle à loi normale était plus approprié pour modéliser le coût risque. Cependant, il est important de noter que d’autres variables explicatives peuvent également jouer un rôle dans la modélisation du coût des sinistres.